百人计划-图形-1.2 数学基础

kio0o0 发布于

最后更新于

求知若饥，虚心若愚

1.2.1 向量基础

摸下🐟，放上大佬的笔记，以及向量相关的其他课程
关于向量的几何意义
  • 向量的标准化normalize，在图形学中十分常用，用来得到只有方向信息且长度为1的向量，比如法线、灯光方向、视角方向等等
  • 向量与标量的计算：只能乘除，不能加减。保持向量方向不变，放大或缩小向量的长度。印象中视差贴图有对向量进行放缩来启发式找到对应视点所在纹理的操作。
  • 点乘：结果为标量，视频中指其意在表明两个向量的“相似”程度，点乘结果越大，夹角越小，反之亦然。另一种通用理解是，向量对另一个向量的单位向量的投影，再乘上其模长，投影有正负以及长度从而能体现出“相似”程度。由于图形学中的向量很多都是单位向量，点乘也能用来求向量夹角的cos值，渲染方程中有体现。值得一提的是点乘符合交换律，即无论谁对谁投影其值都一样，几何上的推导和对偶性有关。
  • 叉乘：叉乘的结果仍是向量，方向与进行计算的两个向量两两垂直，长度为两向量围成的平行四边形的面积，这一块在线性代数的本质视频中有推导。不符合交换律，因为不同的顺序方向将不一样，方向还与左/右手坐标系的定义有关。常见的用法有计算副切线、判断一个点在不在三角形内部。
实现半兰伯特光照模型

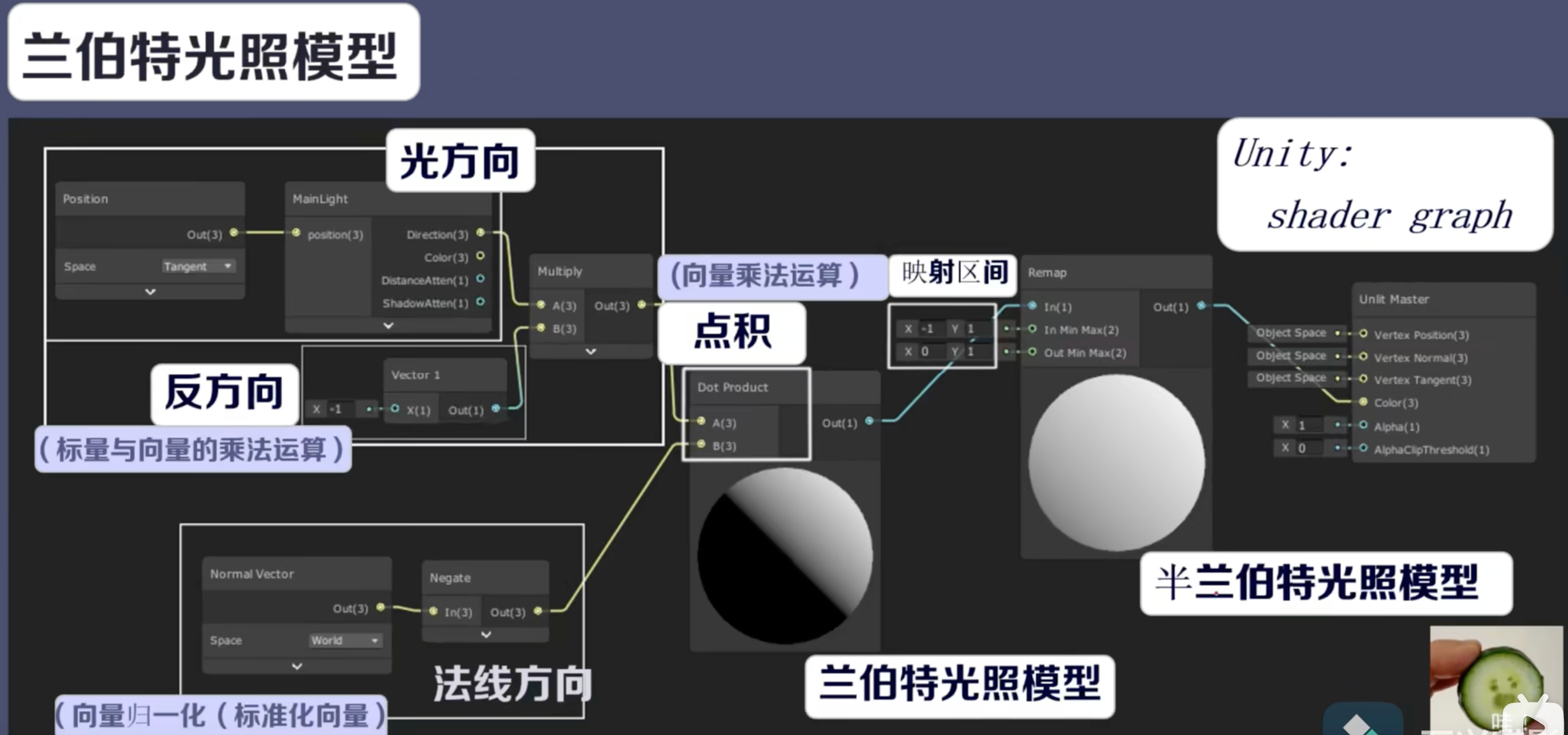
1.2.2 矩阵运算

可供参考的笔记

1.2.3 MVP矩阵运算

参考链接
不同的坐标系
  • 模型空间：以模型自身为原点的局部坐标系。
  • 世界空间：一个场景（舞台）有个中心点，即原点，在场景中的物体都有一个关于那个原点的相对坐标，称为世界坐标系。
  • 视觉空间（观察空间）：以摄像机为原点的坐标系，描述场景中的物体相对于摄像机的关系，从而来判断画面的远近、遮挡、是否显示等关系。需要注意的是视觉空间一般是右手坐标系。
  • 裁剪空间：为投影做准备，进行投影矩阵（裁剪矩阵）变换后，通过坐标值与w分量的对比，舍弃掉不在视锥体范围的顶点，会在交界处生成新的顶点。
  • 屏幕空间：先进行透视除法到NDC坐标，最后屏幕映射到屏幕坐标系（与分辨率大小有关），得到的xy坐标即和屏幕上显示的位置一致，保留z分量来进行深度测试。
  • 需要注意的一点是通常的变换操作有缩放、旋转、平移，由于这三种变换都是相对于原点来说，所以不同顺序的组合会导致不同的结果，我们通常约定要按缩放-旋转-平移来进行变换，避免出现不想要的结果。顺序之所以重要，原因之一就是像旋转和缩放这样的转换是相对于坐标系原点进行的。 缩放以原点为中心的对象产生的结果不同于缩放远离原点的对象所产生的结果。 同样，旋转以原点为中心的对象产生的结果不同于旋转远离原点的对象所产生的结果。
  • 关于旋转矩阵的一种思路（来自3Blue1Brown）：变换基坐标系，假设原坐标系是(1,0)(0,1)，可以在原坐标系找到x轴y轴变换后的向量(cosa,sina)(-sina,cosa)，如果以变换后xy轴形成一个新坐标系，那么其实某个点的表示还是(x,y)，因为坐标系变了，里面的点也跟着变，而原表达式不变。而通过变换后的xy轴向量可以得到新坐标系到原坐标系变换的矩阵（将x轴坐标写在第0列，y轴坐标写在第1列），新坐标系的点通过坐标系变换矩阵就可以得到变换后在原坐标系中的位置。
坐标系变换
  • model transform，相当于拍照时将每个物体找好合适位置并摆Poss（旋转和缩放）
  • view transform，相当于拍照时相机找好角度去拍
    • 有个约定俗成的事情，将相机变换到坐标系原点，且相机的xyz轴和世界的xyz轴对齐（右手系是-z），对其他物体也进行这个变换（相对运动），这样比较方便理解
    • 先进行平移变换到原点，再进行旋转对齐坐标轴。但相机变换到世界坐标轴不好写，可以反过来写世界坐标轴变换到相机坐标轴，再通过逆变换得到矩阵。（由于是正交矩阵，逆矩阵可以通过转置矩阵得到）
  • projection transform，相当于拍照时按下快门成像（推导出自GAMES101-4）

    • orthography projection，将观察空间映射到 标准立方体中，矩阵如下（右手系），一般来说通过view变换已经在原点了，然后再进行缩放变换（所以通常view和projection一起进行，称为viewing变换）。这里需要注意右手系和左手系，n和f谁大谁小可能不一样，z分量需要注意符号

    • perspective projection，将平截头体这种观察空间映射到 标准立方体中，直接写比较困难，可以分解成两步，第一步先将平截头体变成长方体，第二步再进行正交投影。第一步变换中，我们约束两个事情，近平面的点经过变换后保持不变，远平面的中心点经过变换后也保持不变。

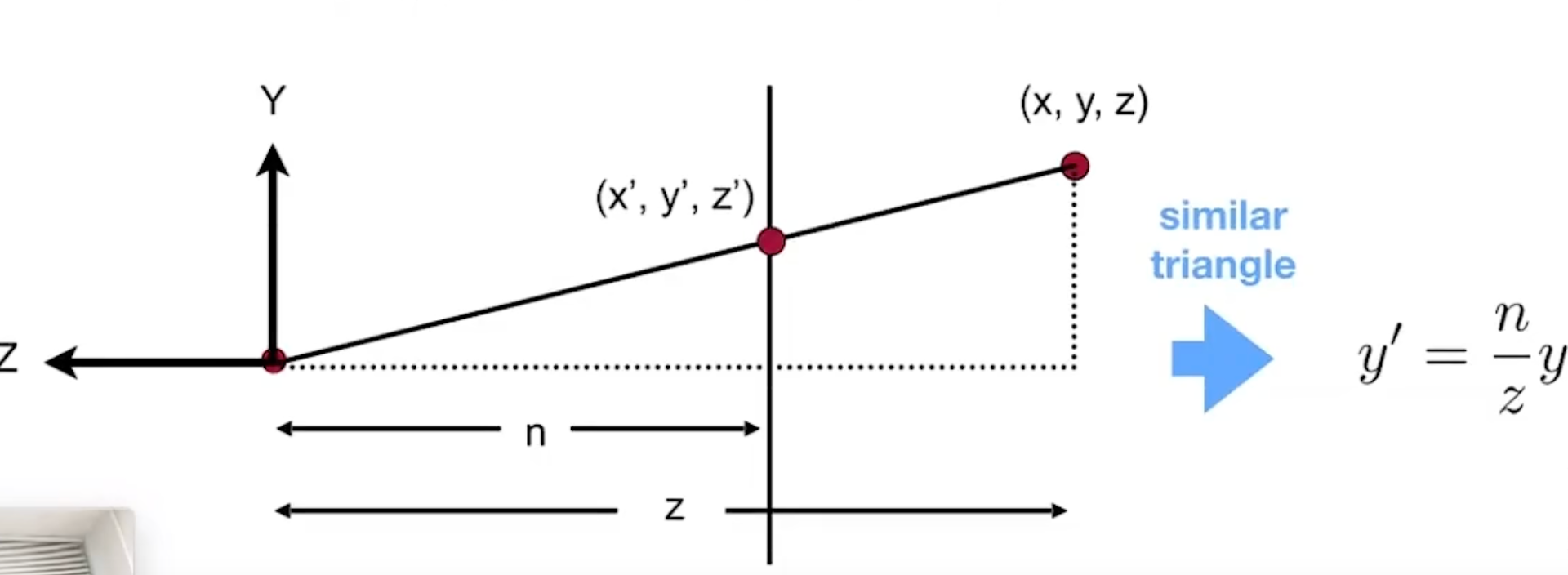
      通过相似三角形观察到，xy如何变换

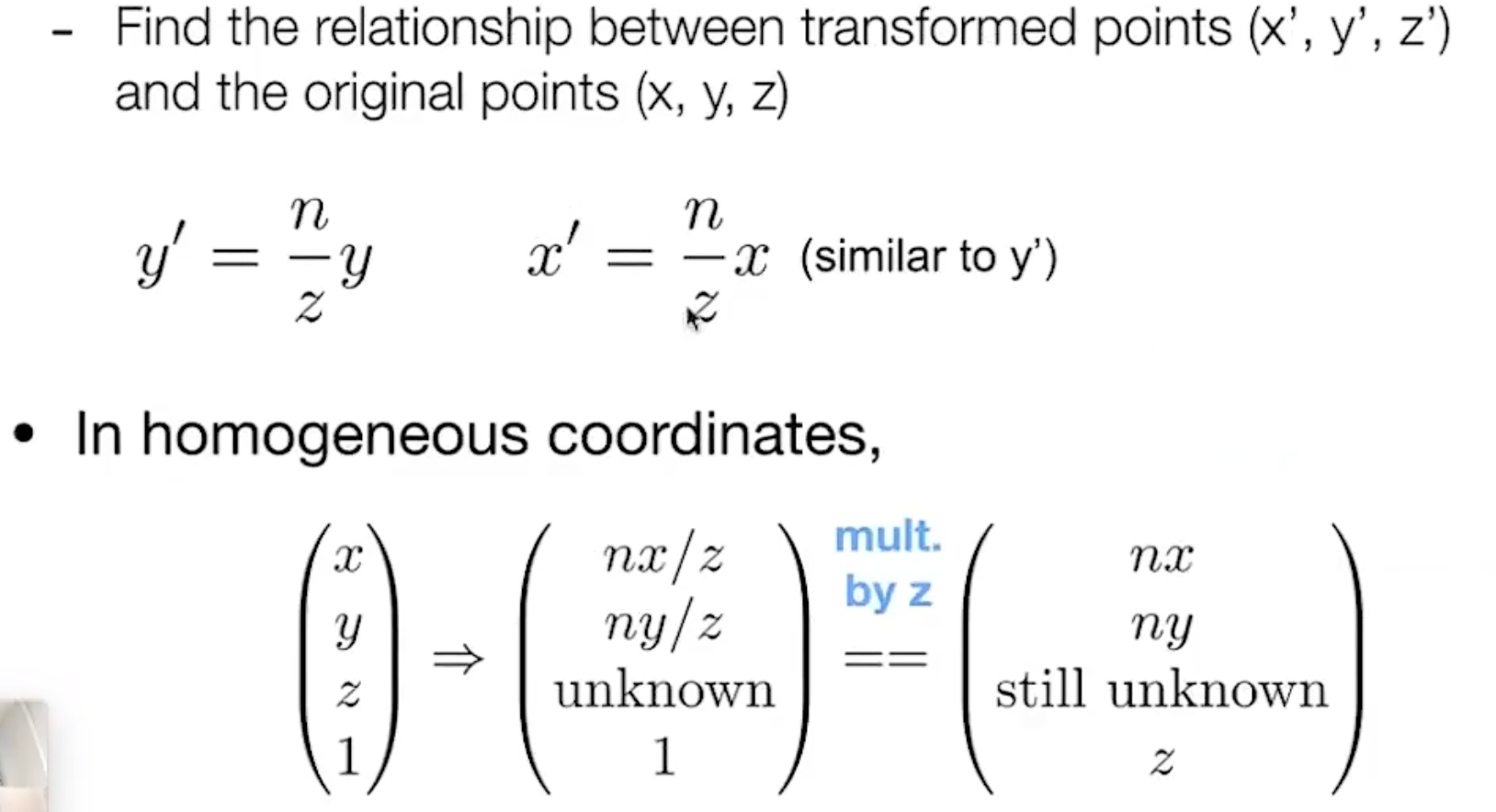
      通过上面对xy的变换初步得到矩阵，此时还有四个未知数

      应用我们上面提到的两个约定，解方程得到四个未知数


      得到透视到正交的变换矩阵后，再进行正交投影即可得到透视投影矩阵

提供一个光栅化的动画演示

www.zhihu.com/zvideo/1347581841478709248

kio0o0

kio0o0

如果可以做到不懂就问，做不到的事情就拒绝，或许可以活得更轻松点

107
6
27
NOTICE

正在努力学习图形学中！

CATEGORYS
TAGS
AMD OS X C#笔记 Github技巧 Hackintosh Lua笔记 Unity Unity Shader入门精要 c++笔记 cocos c语言笔记 drcom shader 代码设计 卡通渲染 图形学 学习 平板 性能优化 搞机 数据结构 游戏开发 百人计划 解题 计划 设计模式 路由器 重构