求知若饥，虚心若愚

笛卡尔坐标系

• 基矢量：坐标系中的坐标轴
• 正交基：坐标轴两两垂直但长度不为1
• 标准正交基：坐标轴两两垂直且长度都为1
• 左手坐标系和右手坐标系，unity除了观察空间都是左手坐标系（将z分量取反可以互相转换，有专门的矩阵变换）。无论使用哪种坐标系，绝大多数情况下并不会影响底层的数学运算，只是映射到视觉上会有差距。

点和矢量

矢量：与标量区分，既有模长（大小）又有方向，与位置无关

矢量运算

• 矢量和标量乘法、除法
• 矢量的加法、减法
• 矢量的模
• 单位矢量、零矢量
• 矢量的点积（几何意义上是一个矢量在另一个矢量的投影，游戏中可用于判断敌人是否在可视范围内、或者在图形学中使用）

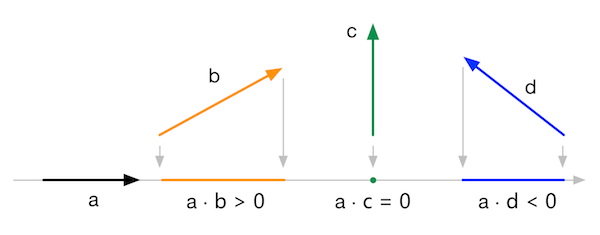
• 矢量的叉积（得到一个垂直于这两个矢量的新矢量）用于计算垂直矢量或者三角面的朝向，方向由对应坐标系的法则结合点的顺序判断

三维矢量叉积的计算规律。不同颜色的线表示了计算结果矢量中对应颜色的分量的计算路径。以红色为例，即结果矢量的第一个分量，它是从第一个矢量的y分量出发乘以第二个矢量的z分量，再减去第一个矢量的z分量和第二矢量的y分量的乘积

矩阵

和矢量的联系

矢量既可以表示成行矩阵也可以列矩阵，unity一般用列矩阵表示，并于内置转换矩阵右乘

矩阵运算

矩阵乘法：必须第一个矩阵的列数和第二个矩阵的行数相同，矩阵计算满足结合律但不满足交互律，得到的新矩阵第i行第j列的结果如下：

特殊矩阵

• 方块矩阵

  行和列都相同的矩阵，三维渲染里最常用的有3 × 3和4 × 4方阵。如果一个矩阵除了对角元素外的所有元素都为0，则称为对角矩阵。

• 单位矩阵

  特殊的对角矩阵，对角元素为1，满足任何矩阵和它相乘的结果还是原来的矩阵

  

• 转置矩阵

  对一个原矩阵进行转置运算的结果即原矩阵的转置矩阵。将原矩阵翻转，即第i行变成了第i列，第j列变成了第j行。

  

• 逆矩阵

  不是所有的矩阵都有逆矩阵，该矩阵必须是一个方阵，逆矩阵满足：

  

  逆矩阵可以撤销原矩阵的变换，逆矩阵满足以下性质：

  

• 正交矩阵

  是一个特殊的方阵，如果一个方阵M和它的转置矩阵的乘积是单位矩阵的话，那么这个矩阵就是正交的。这和逆矩阵的一个性质很像，所以如果一个矩阵是正交的，那么它的转置矩阵就是它的逆矩阵，这对于求逆矩阵可以节省很多计算量。

  

  经过推算当满足以下条件时，该矩阵就是正交矩阵（标准正交基完美满足）
  • 矩阵的每一行都是单位矢量，即与自己的点积为1
  • 矩阵的每一行的矢量之间两两垂直，即互相之间的点积为0
  • 上述结论对矩阵的每一列也成立

行矩阵还是列矩阵

在Unity常规做法是把矢量放在矩阵的右侧，即把矢量转换成列矩阵来计算。即矩阵乘法都是右乘（当然如果避免计算转置矩阵时可以左乘），阅读顺序都是从右到左。下面两个式子是等价的。

矩阵的几何意义：变换

线性变换

可以保留矢量加和标量乘的变换

线性变换主要是旋转和缩放，当然还有错切、镜像、正交投影。线性变换可以用一个3x3矩阵表示


仿射变换：合并线性变换和平移变换，需要用4x4矩阵表示，需要将矢量扩展到齐次坐标空间表示


关于平移矩阵、缩放矩阵、旋转矩阵请查阅相关资料


在Unity中，由于矢量表示为列矩阵，绝大多数情况下，都是右乘操作，阅读顺序从右到左，约定的变换顺序一般是先缩放再旋转最后平移

坐标空间

对坐标空间的变换实际上就是在父空间和子空间之间对点和矢量进行变换

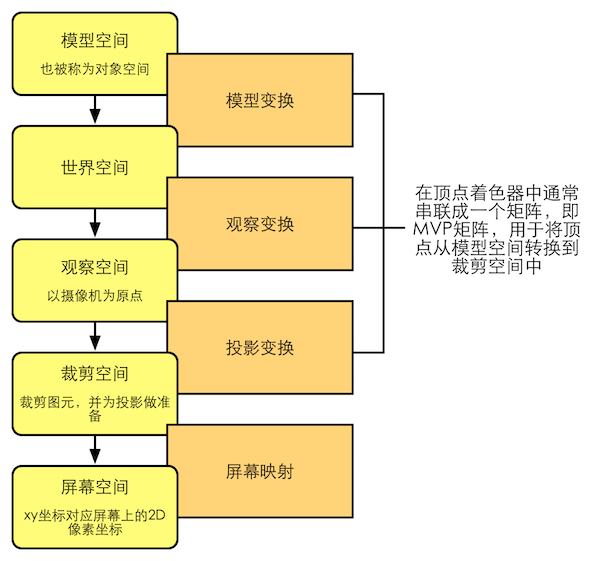
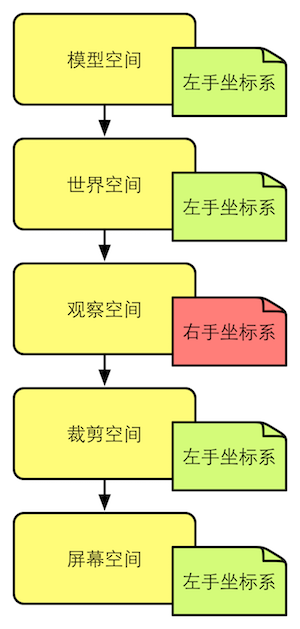
关于裁剪空间的转换涉及到投影，这块要加重了解下投影矩阵的推导、另一篇推导。

法线变换

• 变换法线的时候用同一个变换矩阵可能无法维持法线的垂直性
• 经过推导使用原变换矩阵的逆转置矩阵来变换法线即可得到正确的结果
• 由前面可知，如果变换矩阵是正交矩阵，那么可以直接用这个变换矩阵来变换法线（转置的转置或者说逆矩阵的逆矩阵还是原矩阵）。